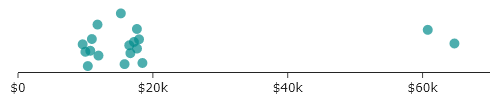Ordering of objects #

~8 minute read

When you put objects down onto the page, you have two options:

You can just slap them down randomly.
You can arrange them in a way that conveys meaning and helps other understand what you are saying. I am going to recommend you take the 2nd option.

Time and space are experienced sequentially #

This simple fact is one we must deal with in designing graphical objects. It also means that, when we put objects on the page, we have an opportunity to consider how one might arrange these objects on the page. While it might seem that there are a very large set of possibilities for arranging things, in reality, there is only a surprisingly small number. This is an idea that designers sometimes call the “five hat racks.”

Five hat racks #

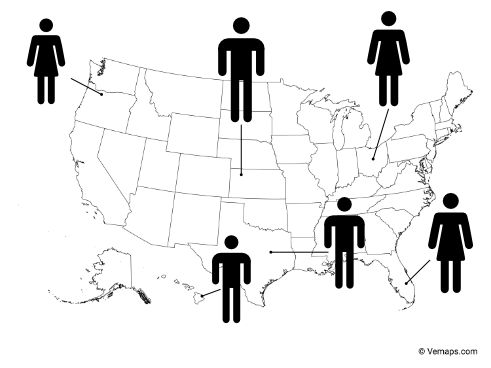
This expresses the idea that, given a set of objects, there are only 5 ways to logically order them. Consider athletes at a event (maybe the Olympics), for instance. The 5 ways we can organize them are:

Chronologically. We could arrange all the athletes by their age, or the date at which they started competing in their event.
Alphabetically. We could arrange all the athletes by their last name, alphabetically.
By magnitude. We could arrange the athletes by height, or weight, most medals won, or furthest distance travelled. As long as we can quantify something about them, we can order by that quantity.
Geographically. One could take a map of the world, and then place each athlete where they currently reside. This is an ordering of the people.
Categorically. We could arrange them by some sort of non-quantitative property.. Perhaps male and female, or by the type of medal they won, or by the country of origin.

Now, spend some time trying to think of other ways that you could organize the athletes, and for each one you arrive at, ask if this arrangement falls within one of the 5 hat racks. You will almost invariably find out that they do. Almost (see below).

Five hat racks in Data visualization #

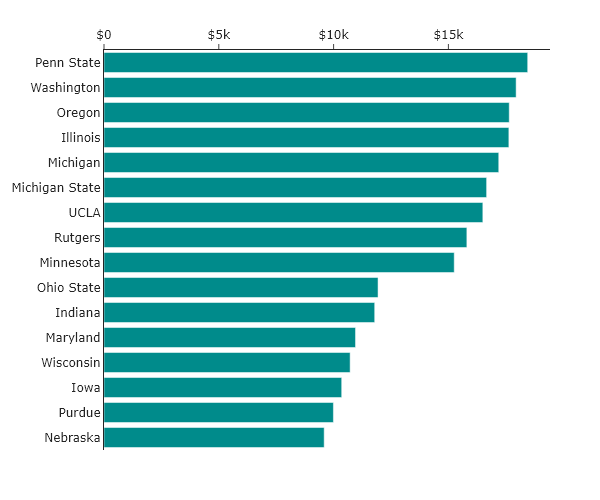
Consider in-state tuition at the Universities belonging to the BIG10 conference in the USA. Imagine you wanted to make a bar chart, and you pulled the data for this, and plotted it without considering the order. You would get a randomly ordered set of bars, much like the following.

Bar chart, showing the tuition costs associated with each of the universities in the BIG10 conference. The bars are in apparently random order.

This data visualization has all the information we might want, but it does not make it easy to find any particular set of data or trend. So, we can consider what we might be interested in seeing, and re-order the bars in response.

Chronological #

One way to think about these schools is when they were founded, or when they joined the big ten. We can order the bars in chronological order, by founding date, and we have the following:

Bar chart, showing the tuition costs associated with each of the universities in the BIG10 conference. The bars are ordered by the year the university was founded.

Now, one can look at this plot and determine if there is a pattern in terms of year founded. There clearly is not, but we can see this directly, in a way that we could not before.

By magnitude #

Perhaps we think the most important aspect of the plot is understanding which Universities are the most and least expensive. The simplest way to do this is to arrange the universities by cost. Ordering by this magnitude results in the following:

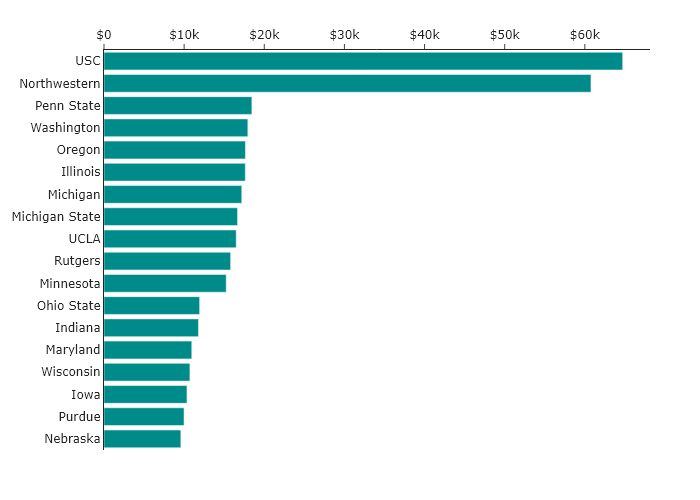
Bar chart, showing the tuition costs associated with each of the universities in the BIG10 conference. The bars are ordered from most expensive to least expensive.

Whereas the two different orderings above made it very hard to tell if, for instance, Wisconsin was more expensive than Maryland, now we can just directly read this from the chart!

Alphabetical #

What if we thought that the person reading the data visualization would be most interested in a particular school, but we didn’t know ahead of time which one? Then the simplest way to find it might be by sorting them alphabetically.

Now it is much easier to find the school of interest, but it is harder to tell what is more expensive than any other school

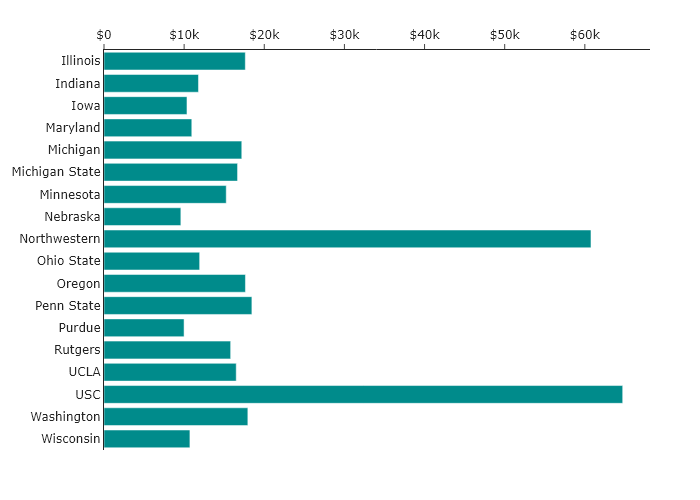
Geographical #

Of course, alphabetical may not be the simplest way for someone to find the University of interest. For instance, how should one sort them. Is “The University of Indiana” be sorted by “T”, or “U”, or “I”? Probably “I” is the most useful, but there is some ambiguity. However, for someone with a reasonable knowledge of the geography of the United States, there is no ambiguity about where Indiana is on the map. By placing the Universities over their location on the map, one can understand where to find them, perhaps with even less thought.

A map in which the location of the BIG10 universities are indicated.

Also, such a map demonstrates the historical origins of the BIG10 among the Public Universities of the midwest. So, this ordering also shows additional information.

Categorical #

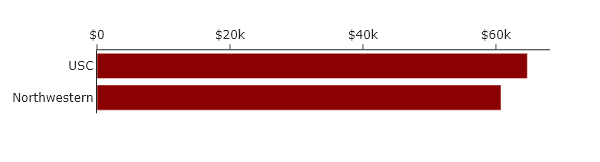
For this specific case, categorical may not be quite as useful as the other orderings, however, the BIG10 does contain both public and private universities, and so one could also imagine making two plots, one that allows comparison between public universities, and one that allows comparison between private universities. This might look like the following:

Bar chart, showing the tuition costs associated with each of thepublic universities in the BIG10 conference.

Bar chart, showing the tuition costs associated with each of the private universities in the BIG10 conference.

Where the ordering by categories helps compare between universities with very different tuition rates.

A special sixth case for data visualizations #

When not working with data visualizations, it is often not the case that we want a random organization. Such organization lacks meaning, and so is not often used. However, there are times that arranging items randomly is important in data visualizations. For instance, if discussing randomized participants in a trial, you might want to randomize their order, so that you can better anonymize them. Or perhaps you have data arranged along a 1D plot, but the points are overlapping, a common approach to solving this is to add jitter—or random displacement—along a second axis. This randomized displacement allows all points to be seen but the random nature helps make it clear that the 2nd dimension does not carry meaning.

For instance, imagine we arranged the tuition of the schools on a 1D line, just so we can see the spread. Without jitter, we would have the following:

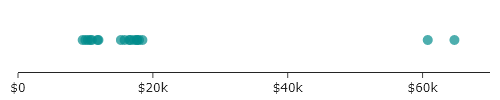
Dot plot showing the tuition for all the universities in the BIG10. Since many of the universities have similar tuition costs, there are many overlapping point.

Though it is a bit easier to see the clustering around values than it was for the bar charts, it is hard to see all the points. If, however, we add in random displacement along the y-axis, we can attain:

Dot plot showing the tuition for all the universities in the BIG10. “Jitter” has been added to the y-axis, so that points with similar tuition can be seen.

Where it is much easier to see all the the points.

Thus, though you will mostly be using the 5 hat racks in organizing your data, there are times you need to reach for this randomization. The main point is to be sure to think about how you arranging things. If you think about it, and decide that random is the best, then go head and do it. What you want to avoid is just accepting the default ordering without question.

Concluding thoughts #

If you are putting things onto a page, you are going to have to arrange them in some fashion. You might as well think about the meaning you are trying to convey, and then order your data accordingly.